引子:你是不是也掉进过“直觉”的陷阱?
想象一个场景:你去做一项疾病检测,这种病的真实发病率(Base Rate)很低,大约只有 1%。医院告诉你,这个检测的准确率高达 99%(无论是真有病诊断为有病,还是没病诊断为没病,判断正确的概率都是99%)。现在,不幸的是,你的检测结果呈阳性。
请问,你真的患上这种病的概率是多少?
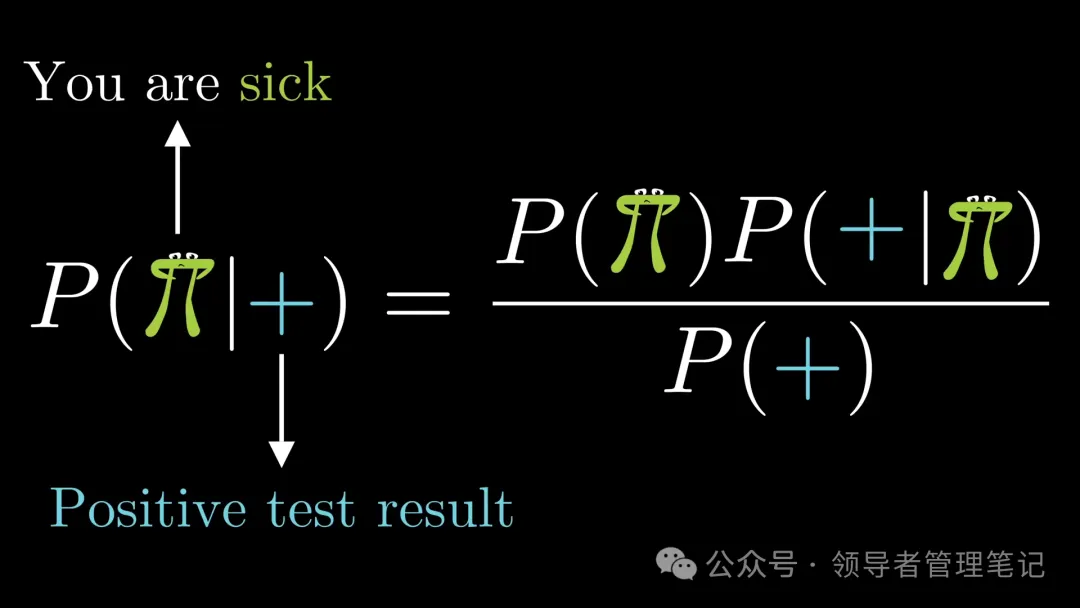
凭直觉,你可能会想:“准确率99%呢!那我肯定是‘中招’了,概率高达99%吧?”
打住。如果真是这样,那这篇文章你可能就不需要往下读了。但现实是,这个“直觉”很可能让你陷入了巨大的恐慌,而真相,远非如此。
为什么我们的直觉会在这里“失灵”?我们又该如何更科学、更理性地看待这个世界的不确定性?
今天,我们就来聊聊一个强大的思维工具,一个能帮助我们穿越“直觉迷雾”,提升决策质量的底层逻辑——贝叶斯公式 (Bayes’ Theorem),也叫贝叶斯定律(贝叶斯定理)。
1、贝叶斯公式,到底是什么?
别被“公式”两个字吓跑。贝叶斯公式的核心思想,其实非常朴素,甚至可以说是我们日常生活中无意识运用的智慧的“数学化表达”。
它解决的是什么问题?是在获得新的信息(证据)后,如何更新我们对某件事情发生的可能性的判断。
简单来说,就是用“过去”的经验,结合“现在”的证据,来预测“未来”的概率。
我们先来看一眼这个公式长什么样(别怕,我们后面会用大白话拆解):
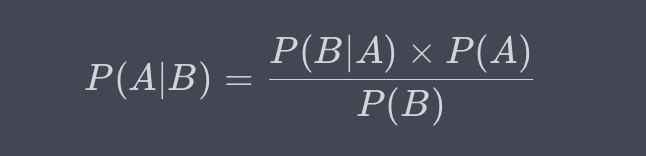
是不是有点懵?没关系,我们把它翻译成“人话”:
1,P(A|B):这个叫做后验概率 (Posterior Probability)。它表示:在事件 B 发生(你看到了新证据 B)的前提下,事件 A 发生(你关心的那个假设 A 成立)的概率是多少?
* 对应到开头的例子:在“检测结果为阳性”(事件 B)的前提下,“你真的患病”(事件 A)的概率是多少?这就是我们最终想知道的答案。
2,P(A):这个叫做先验概率 (Prior Probability)。它表示:在没有任何新证据(B)之前,你对事件 A 发生的可能性的初始判断。这通常基于历史数据、背景知识或普遍认知。
* 对应到开头的例子:就是这种疾病的基础发病率,即 1% (0.01)。这是在做检测前,我们对“任何一个人患这种病”的概率判断。
3,P(B|A):这个叫做似然度 (Likelihood)。它表示:如果事件 A 真的发生了(假设你真的有病),那么你观察到证据 B(检测结果为阳性)的概率有多大?
* 对应到开头的例子:就是检测的准确率,如果真有病(A 发生),检测出阳性(B 发生)的概率是 99% (0.99)。这个指标衡量的是“模型”(检测方法)本身的性能。
4,P(B):这个叫做证据的概率 (Probability of Evidence)。它表示:不管事件 A 发生与否,你观察到证据 B(检测结果为阳性)的总体概率是多少?它是一个“标准化常量”,确保最终计算出的后验概率在 0 到 1 之间。
* 对应到开头的例子:检测结果呈阳性的概率是多少?这需要考虑两种情况:① 你真的有病,且检测为阳性;② 你其实没病,但被误诊为阳性。所以 P(B) = P(B|A) * P(A) + P(B|非A) * P(非A)。

2、拆解公式,理解“动态认知”的底层逻辑
现在,我们把开头的例子代入公式算一下:
- P(A) = 患病的基础概率 = 1% = 0.01
- P(非A) = 不患病的基础概率 = 1 – P(A) = 99% = 0.99
- P(B|A) = 真有病时,检测为阳性的概率(真阳性率) = 99% = 0.99
- P(B|非A) = 没病时,检测为阳性的概率(假阳性率)= 1 – 99% = 1% = 0.01 (因为准确率是99%,没病判断为没病的概率是99%,那么没病判断为有病的概率就是1%)
我们想求的是 P(A|B),即检测为阳性时,你真患病的概率。
首先计算 P(B),即检测结果为阳性的总概率:
- P(B) = P(B|A) * P(A) + P(B|非A) * P(非A)
- P(B) = (0.99 * 0.01) + (0.01 * 0.99)
- P(B) = 0.0099 + 0.0099
- P(B) = 0.0198
然后,套用贝叶斯公式:
- P(A|B) = [P(B|A) * P(A)] / P(B)
- P(A|B) = (0.99 * 0.01) / 0.0198
- P(A|B) = 0.0099 / 0.0198
- P(A|B) = 0.5
看到结果了吗?只有 50%!
跟你直觉的 99% 是不是差很远?为什么会这样?
这就是贝叶斯思维的威力所在。它告诉我们:不要忽视基础概率(先验概率 P(A))!
在这个例子里,虽然检测很准 (P(B|A) 很高),但因为基础发病率本身极低 (P(A) 很低),即使检测结果是阳性,这个结果有相当大的可能性(在这个例子里是 50%)是由那极少数的“假阳性”贡献的 (P(B|非A) * P(非A))。
贝叶斯公式的本质,是一种动态更新认知的过程:
初始信念 (先验概率) + 新证据 (似然度) → 更新后的信念 (后验概率)
它承认我们最初的判断可能不完美(先验),但它提供了一个数学框架,让我们能够理性地、定量地结合新出现的信息(证据),来不断修正和优化我们的判断,使其更接近真相。这是一种基于证据的、迭代式的认知升级。
3、贝叶斯思维,如何赋能商业与生活?
理解了贝叶斯公式的原理,你可能会问:这东西除了做数学题,还有什么用?
用处大了去了。贝叶斯思维,几乎可以渗透到我们工作和生活的方方面面,帮助我们做出更明智的决策:
1. 商业决策 – A/B 测试效果评估:
* 你上线了一个新功能,做了 A/B 测试,发现实验组(使用新功能)的转化率比对照组高 5%。这个结果可靠吗?能直接推广吗?
* 贝叶斯方法可以结合你对新功能效果的先验判断(比如,根据经验,大部分改动效果甚微),以及这次测试的数据(证据),给出一个更稳健的后验概率——即新功能真正优于旧功能的概率有多大。这比单纯看 p-value 更能指导行动。
2. 投资决策 – 风险评估:
* 一个分析师推荐了一只“潜力股”。他的推荐(证据 B)有多大可信度?这只股票真正有潜力(事件 A)的概率是多少?
* 你需要考虑分析师的历史“命中率”(似然度 P(B|A) 和 P(B|非A)),更要结合你对这只股票、这个行业、乃至整个市场的基础判断(先验概率 P(A))。贝叶斯能帮你整合信息,而不是仅仅被某个“利好消息”冲昏头脑。
3. 产品开发 – 用户需求判断:
* 少数用户的强烈反馈(证据 B)是否代表了大部分用户的真实需求(事件 A)?
* 你需要结合你对目标用户群体的整体认知(先验概率 P(A)),以及这次反馈的代表性(似然度 P(B|A)),来判断是否应该投入资源去满足这个需求。避免被“噪音”误导。
4. 人才招聘 – 面试评估:
* 一个候选人在面试中表现优异(证据 B)。他是否真的是一个高绩效者(事件 A)?
* 面试表现好(P(B|A))固然重要,但也要考虑“面霸”(能力一般但面试技巧好)的可能性(P(B|非A)),以及你对符合该岗位要求的人才在整体市场上的稀缺度(先验概率 P(A))的判断。综合评估,而非“一见钟情”。
5. 日常生活 – 信息辨别:
* 看到一则耸人听闻的新闻(证据 B),它有多大概率是真的(事件 A)?
* 问问自己:这个信息来源的可信度如何(似然度)?这类事件发生的通常概率(先验概率)有多大?是不是太反常识了?用贝叶斯思维过滤信息,能帮你抵抗谣言和假新闻。
4、拥抱贝叶斯,成为更聪明的决策者
贝叶斯公式不仅仅是一个数学工具,它更是一种思维方式,一种认知世界的底层逻辑。它提醒我们:
1. 尊重基础概率 (Base Rate):做判断时,永远不要忽略事物发生的普遍概率。这是我们决策的“锚”。忽视基础概率,是人类常见的认知偏误。
2. 证据的质量很重要 (Likelihood):新信息的“含金量”决定了它能在多大程度上更新我们的认知。证据越可靠,似然度越高,对后验概率的影响越大。
3. 认知是动态迭代的 (Prior → Posterior):没有绝对的“正确答案”,只有基于当前信息的最优判断。我们要拥抱不确定性,并乐于根据新证据不断更新、修正自己的看法。永远保持开放和学习的心态。
5、结语:从一次计算,到一种智慧
回到开头的例子。检测结果呈阳性,患病概率 50%。这个结果告诉你,你需要进一步检查确认,而不是直接陷入绝望。这就是贝叶斯公式带给你的理性。
掌握贝叶斯思维,不是要求你每次决策都拿出纸笔来计算。更重要的是,将这种“先验 + 证据 → 后验”的逻辑内化于心。
当你遇到不确定的情况时,问自己:
- 关于这件事,我之前是怎么看的?(先验概率)
- 这个新信息,告诉我了什么?它有多可靠?(证据和似然度)
- 结合新信息,我现在应该怎么看?(后验概率)
经常这样思考,你会发现,你看待世界的方式会悄然改变。你会变得不那么容易被表象迷惑,不那么容易被情绪左右,决策会更加稳健、理性。
贝叶斯公式,就像一副“认知眼镜”,帮助我们透过现象看本质,在充满不确定性的世界里,持续做出更聪明的选择。
希望你从今天起,开始尝试用这副“眼镜”看待世界。
THE END
转载请注明:好奇网 » 一文搞懂贝叶斯公式:从原理到应用