在数学的发展史上,大大小小的矛盾出现过很多,但很少能威胁到整个数学基础理论,甚至引起危机。即便诸如是千百年来人们对欧几里得几何公理第五公设的疑惑,也不曾造成数学上的危机;且最终成就了罗巴切夫斯基几何和黎曼几何。但数学史上共出现三次对基础理论的正确性造成了威胁的悖论,史称数学危机,每次都是由于悖论的发现而深刻和广泛地影响了数学基础。
- 公元前5世纪——希帕索斯悖论与第一次数学危机
- 17世纪初——贝克莱悖论与第二次数学危机
- 19世纪末——罗素悖论与第三次数学危机
第一次数学危机
公元前5世纪,有理数与无理数
1. 主要内容
大约在公元前5世纪,毕达哥拉斯学派的希帕索斯发现了: 等腰直角三角形的直角边与其斜边不可通约。正是这个不可通约量的发现引发了“第一次数学危机”。
希帕索斯正是因为这一数学发现,而被毕达哥拉斯学派的人投进了大海,处以“淹死”的惩罚。因为他竟然在宇宙间搞出了这样一个东西来否定毕达哥拉斯学派的信条:宇宙间的一切现象都能归结为整数或整数之比。
毕达哥拉斯学派是古希腊最古老的哲学学派之一。据说这个学派有两条最能概括他们思想特色的格言:“什么最智慧? 只有数目”,“什么最美好?只有和谐”。毕达哥拉斯学派在数学上的一项重大贡献是证明了勾股定理,但由此也发现了一些直角三角形的斜边不能表示成整数或整数之比 (不可通约) 的情形,如直角边长均为1的直角三角形就是如此。
直角三角形的直角边与其斜边不可通约,这个简单的数学事实的发现使毕达哥拉斯学派的人感到迷惑不解。它不仅违背了毕达哥拉斯派的信条,而且冲击着当时希腊人持有的“一切量都可以用有理数表示”的信仰。所以,通常人们就把希帕索斯发现的这个矛盾,叫做希帕索斯悖论。
2. 意义
这一悖论的发现,震惊了当时的西方数学界,也引起了古希腊人数学观念的更新。这场“危机”表明,直觉和经验不一定靠得住,推理证明才是可靠的。从此以后,希腊人开始由重视计算转向重视推理,由重视算术转向重视几何学,并由此建立了几何公理体系。其实,这是数学思想上的一次巨大革命!
 第二次数学危机
第二次数学危机
17世纪初,无穷小量的定义
1. 问题的产生
在微积分大范围应用的同时,关于微积分基础的问题也越来越严重。关键问题就是无穷小量究竟是不是零?无穷小及其分析是否合理?由此而引起了数学界甚至哲学界长达一个半世纪的争论,造成了第二次数学危机。无穷小量究竟是不是零?两种答案都会导致矛盾。牛顿对它曾作过三种不同解释:1669年说它是一种常量;1671年又说它是一个趋于零的变量;1676年它被“两个正在消逝的量的最终比”所代替。但是,他始终无法解决上述矛盾。莱布尼兹曾试图用和无穷小量成比例的有限量的差分来代替无穷小量,但是他也没有找到从有限量过渡到无穷小量的桥梁。
英国大主教贝克莱于1734年写文章,攻击流数(导数)“是消失了的量的鬼魂……能消化得了二阶、三阶流数的人,是不会因吞食了神学论点就呕吐的。”他说,用忽略高阶无穷小而消除了原有的错误,“是依靠双重的错误得到了虽然不科学却是正确的结果”。贝克莱虽然也抓住了当时微积分、无穷小方法中一些不清楚不合逻辑的问题,不过他是出自对科学的厌恶和对宗教的维护,而不是出自对科学的追求和探索。这一论点在史上称为贝克莱悖论。
18世纪的数学思想的确是不严密的、直观的,强调形式的计算而不管基础的可靠。其中特别是:没有清楚的无穷小概念,从而导数、微分、积分等概念不清楚;无穷大概念不清楚;发散级数求和的任意性等等;符号的不严格使用;不考虑连续性就进行微分,不考虑导数及积分的存在性以及函数可否展成幂级数等等。
2. 解决与意义
直到19世纪20年代,一些数学家才比较关注于微积分的严格基础。从波尔查诺、阿贝尔、柯西、狄里赫利等人的工作开始,到魏尔斯特拉斯、狄德金和康托的工作结束,中间经历了半个多世纪,基本上解决了矛盾,为数学分析奠定了一个严格的基础。
魏尔斯特拉斯在数学分析领域中的最大贡献,是在柯西、阿贝尔等开创的数学分析严格化潮流中,以ε-δ语言,系统建立了数学分析的严谨基础。在魏尔斯特拉斯的分析体系中可以看出,无穷小不是一个确定的数,而是反映变元或函数的一种状态;无穷小也不是零,但它的极限是零。
魏尔斯特拉斯的工作基本上完成了分析的算术化,加上实数理论、集合论的建立,从而把无穷小量从形而上学的束缚中解放出来。这使数学走向了理性,微积分走向了理论,第二次数学危机基本解决。
第三次数学危机
19世纪末,集合论的基本结构
1. 问题的产生
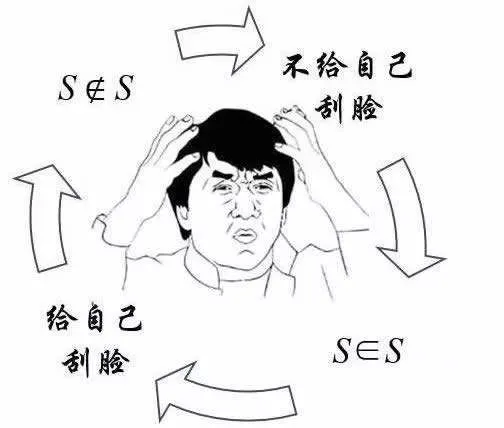
1897年,福尔蒂揭示了集合论中的第一个悖论。两年后,康托发现了很相似的悖论。1902年,罗素又发现了一个悖论,它除了涉及集合概念本身外不涉及别的概念。罗素悖论曾被以多种形式通俗化。其中最著名的是罗素于1919年给出的,它涉及到某村理发师的困境。理发师宣布了这样一条原则:他给所有不给自己刮脸的人刮脸,并且,只给村里这样的人刮脸。当人们试图回答下列疑问时,就认识到了这种情况的悖论性质:”理发师是否自己给自己刮脸?”如果他不给自己刮脸,那么他按原则就该为自己刮脸;如果他给自己刮脸,那么他就不符合他的原则。
对罗素悖论的精确表述为:如果存在一个集合A={X| X∉ A },那么X∈A是否成立?如果它成立,那么X∈A,不满足A的特征性质。如果它不成立,A就满足了特征性质。
对于第三次数学危机,有人认为只是数学基础的危机,与数学无关。这种看法是片面的。诚然,问题涉及数理逻辑和集合论,但它一开始就牵涉到无穷集合,而现代数学如果脱离无穷集合就可以说寸步难行。因为如果只考虑有限集合或至多是可数的集合,那绝大部分数学将不复存在。而且即便这些有限数学的内容,也有许多问题要涉及无穷的方法,比如解决数论中的许多问题都要用解析方法。由此看来,第三次数学危机是一次深刻的数学危机;或者说,直到如今,它仍未被很好地解决。
2. 解决现状与相关结果
经过艰苦的努力,德国数学家哥德尔在1931年取得了突破性进展。他提出了著名的“不完备性定理”,这个定理指出:任何包含算术的形式系统,如果是一致的(即无矛盾的),则必定是不完备的(即存在无法证明也无法证伪的命题)。这一发现震惊了数学界,因为它意味着数学家们不可能构建出一个既完备又一致的形式化数学系统。其他数学家在此基础上通过将集合的构造公理化来排除了这样的集合的存在性。
例如,在策梅洛(Zermelo)和弗伦克尔(Fraenkel)等提出的ZF公理系统(也称ZFC公理系统)中,严格规定了一个集合存在的条件(简单地说,存在一个空集【空集公理】;每个集合存在幂集【幂集公理】;每个集合里所有的集合取并也形成集合【并集公理】;每个集合的满足某条件的元素构成子集【子集公理】;一个”定义域“为A的”函数“存在“值域”【替换公理】等),这样无法定义出悖论中的集合。
随着新的公理系统的建立和应用,数学家们逐渐走出了第三次数学危机的阴影。他们开始重新审视并发展各个领域的数学知识从几何学到代数学从分析学到拓扑学都取得了前所未有的进步和突破。数学的严谨性和实用性得到了极大的提升它再次成为了人类探索自然和社会现象的有力工具。
 总结与启示
总结与启示
数学发展的历史有助于深入理解数学。数学学习中我们经常遇到会有许多如下的疑惑:为什么古希腊数学家喜欢用几何方法研究处理数学问题?为什么把无限不循环小数叫做无理数?数学的理论或结构是如何建构的?为什么要进行证明?通过对三次数学危机发生、发展史的考察,我们对数学的理解能得到提高。相对数学世界的瀚海大海,限于目前已知的狭隘知识面,我们对数学的认知目前还是冰山一角。如果我们能比较全面、系统地了解数学的发展史,无疑能提高我们对数学理解的高度以及深度。
转载请注明:好奇网 » 数学大厦的崩解与重建——三次数学危机